伝送路を伝わる信号の振幅を計算する
伝送路(伝送線路 transmission line)を伝わる信号の振幅は、次に示す式で計算できます。(*1)損失のない理想的な無損失伝送路 (Lossless transmission line)の動作は5番目の式を使わずに簡単に計算できます。
損失のある有損失伝送路 (Lossy transmission line)は少し複雑ですが、係数さえ求めておけば後は同様に計算できます。
-
ダイオード終端は、非線形素子 (non linear element)が関わるため簡単には計算できません。
3番目の式は使わなくても計算できます。
実際の伝送路は損失がありますから、5番目の式は必要です。5番目の伝播係数は、伝送路の抵抗、表皮効果(skin effect)、直列インダクタンス、並列キャパシタンスの効果によるものです。
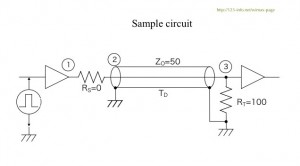
次の条件を設定しました。回路図は図2.1.3a と同じです。
| ZS=0 | 信号源インピーダンス | |
| ZO=50 | 伝送路の特性インピーダンス | |
| ZL=100 | 負荷インピーダンス | |
| VIN=5V | 信号振幅 |
1 入射係数 Input acceptance coefficient
A(\omega)=\frac{Zo}{Zs+Zo}=\frac{50}{0+50}=1
2 近端反射係数 Source-end reflection coefficient
Ref_1(\omega)=\frac{Z_S - Z_O}{Z_S + Z_O}=\frac{0 - 50}{0 + 50}=-1
3 透過係数 Output transmission coefficient
T(\omega)=\frac{2 \times Z_L}{Z_L + Z_O}=\frac{2 \times 100}{100 + 50}=1.33
4 遠端反射係数 Far-end reflection coefficient
Ref_2(\omega)=\frac{Z_L - Z_O}{Z_L + Z_O}=\frac{100 - 50}{100 + 50}=0.333
5 伝播係数 Propagation coefficient
H_X(\omega)=exp({\sqrt{-X(R{\omega}+j{\omega}L) (j{\omega}C)}})
-
ここで、
R=Ω/inch 伝送路の直列抵抗
L=H/inch 伝送路の直列インダクタンス
C=F/inch 伝送路の並列キャパシタンス
ω=2πf 角周波数、
X =inch ケーブル長
1回転は2πラジアンより
ω=dθ/dt = 2π/T=2πf
θ 角度 ラジアン radian
T 周期 秒 second
f 周波数 frequencyそれぞれの式は周波数の関数です。信号源抵抗、伝送路の特性インピーダンス、負荷抵抗の値は周波数と共に変化するからです。(変化しないのが理想ですが現実には不可能です。)
 |
ZS=0, ZO=50, ZL=100, VIN=5V |
3.1.1 送信した信号が伝わるまでの経過
信号源から出た信号は、次のように伝わります。
1. ドライバの信号は、伝送路の入り口では入射係数で決まる振幅になる。
信号は伝送路を伝わり遅延時間を経過した後にレシーバへ届く。
遅延時間は媒体の比誘電率 dielectric constant (relative permittivity)と長さにより変化する。
2. 受信端まで届いた信号は、遠端反射係数=0以外のときはここで反射する。
3. 反射により送信端まで戻った信号は、近端反射係数=0以外のときはここで反射して再び戻る。
戻るまでの遅延時間は送信のときと等しい。
受信端で観測する信号は、以上の経過を経て現れます。
では、この流れを具体的に計算します。
負荷まで伝わる1回目の信号
信号源が送信を開始すると、ノード1の電圧は上昇します。この回路の条件では(1)式の係数=1より 5Vになるのは明らかです。
ノード2の電圧は、信号源インピーダンスが0であることから信号源の電圧がそのまま伝わり、ここで伝送路に入ります。無損失伝送路では信号は減衰しませんから、5Vのままの電圧がノード3まで到達します。
しかし、ノード3で観測する波形は、進行波の振幅5Vではなく、ノード3の反射波を合成したものです。ノード3はZOとは等しくない終端条件であることから、反射波が生じます。(仮に、ZL=ZOの条件では反射係数=0になる)
ノード3に現れる電圧は進行波と反射波それぞれの振幅を加算します。
ノード3に1番目に到達した波形の振幅は、信号源の振幅5Vを超えますが、この現象はオーバーシュート(over shoot)です。1番目のオーバーシュートを計算します。
反射波の振幅は
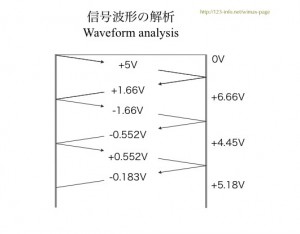
5V \times Ref_2=5 \times 0.333=1.66V (3.1)
進行波の振幅は 5Vであるのがわかりますから、1番目のオーバーシュートは
1.66V + 5V=6.66V (3.2)
または、T(ω)で計算します。(1回目はこの式で簡単に計算できますが、2回目以降は簡単に計算できません。)1番目のオーバーシュートは、
5V \times T(\omega)=5 \times 1.33=6.66V (3.2b)
1回めのオーバーシュートの振幅は6.66Vの大きさであることが、シミュレータの結果(図2.1.3b)からもわかります。信号源から負荷まで伝わる所要時間は、シミュレータで設定した 500nsです。(反射波が戻るのに要する時間も等しい。)
受信端から反射する1回目の信号
1回めの反射波の振幅はすでに求めたとおりです。負荷抵抗は伝送路のインピーダンスと等しくないことから、信号源の方向に反射して戻ります。
- なぜ反射するのか疑問に思う人がいるかもしれませんが、エネルギー保存の法則を考えればわかると思います。エネルギー(この例では正確には電力)はいきなり消滅しません。消滅しないものは送信端に戻るしかないのです。消えないものは反射して戻らないとつじつまが合わない理屈です。
送信端で1回目に反射して進む信号
負荷から反射して戻った信号は、信号源抵抗が0であることからZOと等しくないためここで反射し、再び負荷の方向へ進みます。反射係数Ref1=1より、100%の振幅を反射します。すなわち反射波の振幅は
1.66V \times Ref_1 =1.66V \times -1=-1.66V (3.3)
再び負荷まで到達した信号は、また反射します。そのときの反射波の振幅は
-1.66V \times Ref_2 =-1.66V \times 0.333=-0.552V (3.4)
この時点でノード3で見える2番目の波形(アンダーシュート under shoot)の振幅は、ノード3に現れた今までのものをすべて合成した値です。つまり
5V + 1.66V -1.66V -0.552V=4.448V (3.5)
信号が何度も反射する様子は、オーバーシュートまたはアンダーシュートがなくなるまで続きます。
受信端に現れる信号
以上のように、それぞれの部分は計算式で求めることができます。
受信端で観測する波形は、進行波と反射波の合成を累積したものです。
信号波形は以上の動作を繰り返したものから求めることができます。ここで計算した値と回路シミュレータが描いた波形は正確に一致することがわかります。
なお、立ち上がり時間=0で設定したほうが波形はわかりやすいかもしれません。
-
立ち上がり時間 0の信号をグラフで表すと90°になります。こんな信号は現実には存在しません。なぜなら無限大の周波数成分を含むからです。
蛇足ながら、「波形」は便宜的な表現です。振幅対時間で表すと波形ができるのであり、2次元の形が実際にある訳ではなく、信号そのものは電気的な強弱にすぎません。
同じ信号でも「波形」を観測するときの視点をどこから見るかにより信号の形は変化します。時間軸(time domain)を視点にするだけではなく、周波数軸(frequency domain)で観測する方法もあります。
3.2 伝送路を伝わる信号を図で求める
信号の振幅は計算式で求めることもできますが、もっと簡単に求める方法があります。反射を繰り返す様子を図にしたものがラティス・ダイアグラム (Lattice diagram)です。
この図では、信号波形の振幅をもっと簡単に計算できます。右側の値は受信端に現れる振幅で、累積した値を示すことがわかります。
 |
- 参考資料
-
*1
High Speed Digital Design A Handbook of Black Magic
H. W. Jhonson, M. Graham Prentice-hall 1993