──────────────────────────────────────
<更新情報>
2012年11月3日
ディジタルオーディオ放送の説明で分かりにくい部分があり、説明を追加
しました。
2012年11月4日
変調方式の図について、分かりにくい部分があり入れ替えました。
──────────────────────────────────────
ディジタル変調の目的
ディジタル変調 (Digital Modulation)は、伝送したいディジタルデータにより搬送波を変調します。送信機は変調した波形を電波(電磁波)信号にしてアンテナから空間に送出します。電波は空間を伝わり受信機に届きます。(電波は何も存在しない真空中でもエネルギーが伝わる物理現象です。)
変調後の信号はアナログ波形です。(念のため強調しておきますが、ディジタル信号ではありません。)目的は、ディジタルデータを効率良く伝送することにあり、変調方式の違いにより伝送効率は異なります。
搬送波(carrier)は、伝送媒体(メディア)そのものです。たとえばWiFiでは2.4GHzまたは5GHzの周波数帯にあるチャンネル周波数です。
「ディジタル変調」を一言で表現すると、「信号処理によりディジタル信号をアナログ信号に変換すること」です。
「変調」を利用する伝送方式は、「ベースバンド伝送」と対比します。高い効率を備えた変調による伝送方式は、同じ条件でベースバンド伝送よりも一度に大量の情報を届けることができます。
- ベースバンド伝送
- ベースバンド伝送 (Baseband Transmission) は、ディジタルデータを変調せずに伝送する方式です。具体的にはイーサネットやUSBはこれに該当します。しかし、データをそのまま伝送することはしません。生のディジタルデータの伝送はエラーの発生率が大きいからです。そこで、符号化してから送信します。受信側は、復号してからデータを取り出します。
たとえば 100BASEは4B/5B符号、1000BASEは8B/10B符号を使います。USB2.0はNRZI 符号で、USB3.0 は8B/10B符号やPRBS (Pseudo Random Bit Sequence) を使います。
符号については、伝送データの符号化を参考にどうぞ。
- 光通信
- 光ファイバによる通信は電気ワイアのイーサネットなどとは異なります。ベースバンド伝送ではなく、波長多重 (Wavelength Division Multiplexing) や偏波多重 (Polarization Multiplexing) などの技術により伝送容量(速度)を高めています。こちらは、機会をみて記事にします。
- FMラジオ放送とディジタル変調による放送
- 余談ですが、FMラジオ放送のxxMHzというときは、搬送波の周波数を表します。FMラジオは音声や楽器などの可聴帯域の信号でそのまま変調しますからアナログ変調です。
衛星回線で放送していたミュージックバード(CS-PCM方式)は、ディジタル化した信号(=ディジタルオーディオ)ですが、こちらはディジタル変調(電波で通信するときはアナログ信号)です。復調してからDA変換器 (Digital to Analog Converter)によりアナログ信号に変換します。(CS-PCM放送は2011年7月に終了しました。)
ミュージックバードは社名でもありますが、現在はCS-PCM放送の後継とも言えるSPACE DiVAを放送しています。ディジタル変調である点はCS-PCMと同じですが、MP2(MPEG-1 Audio Layer2)フォーマットで、圧縮してあるところがが少し違います。
ディジタルオーディオの伝送規格も国際標準化が行われています。機器間の有線通信では符号化したディジタルのベースバンド伝送である点は、USBやイーサネットなどと共通です。
ディジタル変調の方式と変調後の波形
伝送するデータは、搬送波(carrier)という信号にのせて運びます。このとき、データをのせる最小単位(時間)を「シンボル」と呼びます。一つのシンボルにいくつのデータを乗せるのか、これがシンボルレート(変調速度)です。シンボルレートを高くすると一度にたくさんのデータを伝送できます。
変調方式はいくつもありますが、シンボルレートで大きく分けると次の2種類です。
・2値変調(最も基本的な方式)
・多値変調
「2値変調」は1つのシンボルあたり1ビットを伝送できます。たとえば、次の「2値変調の方式」の3種類のどれでも1つのシンボルはデータ「0」または「1」を伝送することができます。
「多値変調」は1つのシンボルあたり複数のデータを伝送でき、伝送効率は上がります。しかしいいことばかりでありません。ノイズによる伝送エラーの確率は2値変調でさえ0ではなく、多値変調ではさらに増加します。誤りを検出し訂正 (Error Detection and Correction) すると、この処理を追加しても全体の伝送効率を上げることができます。
変調方式の詳細については、続きをどうぞ。
2値変調の方式
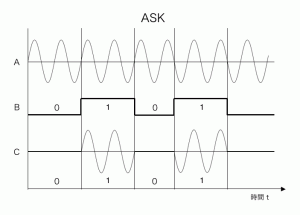
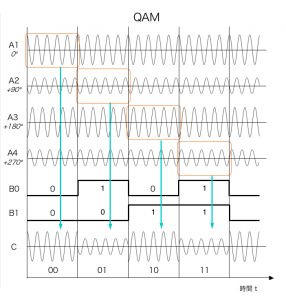
まず、2値変調です。下記のそれぞれの図で、最も下にある「C」がそれぞれ変調後の波形です。送信機から放射する電波に変わる前の信号を、時間軸対振幅で観測するとこんな格好をしています。
ただし、あくまで模式図であり、ここでは分かりやすく説明するために時間軸(水平方向)を拡大していますが、現実の機器では、波形の周期はまったく異なります。個々の波形は時間軸方向に拡大しないと見えないことが多いと思います。さらに、受信側で観測するとノイズの影響を受けるので大きく崩れることも多く、元の波形がそのまま見えるとは限りません。
| 図 ASK | 図 FSK |
 |
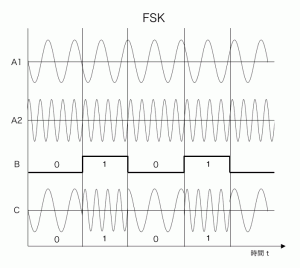 |
| 図 PSK | |
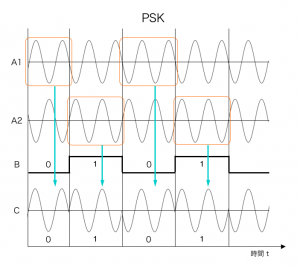 |
多値変調の方式
同じ帯域幅で、たくさんのデータを乗せるには多値変調を使います。
「位相変調」(PSK) は、信号の位相情報(位相角、振幅を表す同心円は一つのみ)を利用しディジタルデータを乗せます。PSKは基本であるBPSK (Binary PSK) 以外に、QPSK (Quaternary PSK 4値位相変調) や8PSKのように応用することができます。
QAMも「多値変調」の一種です。QAMは、16QAM、32QAM、64QAM、256QAMのように種類があります。
| 変調方式 | 説明 | |
| ASK | Amplitude-Shift Keying 振幅変調 | |
| FSK | Frequency-Shift Keying 周波数変調 | |
| PSK | Phase-Shift Keying 位相変調 | |
| n-PSK | n-Phase Shift Keying 基本のBPSKは、位相差が180°の2種類の搬送波を用意し、ベースバンド信号の「1」と「0」で切り替える。n-PSKは、位相差が複数の搬送波を用意し、データを乗せる。 |
|
| n-QAM | n-Quadrature Amplitude Modulation 直角位相振幅変調 位相と振幅の異なる搬送波を用意し、組み合わせてデータを乗せる。 |
紛らわしく感じるかもしれませんが、QPSKとQAMの「Q」は異なる単語です。文献により、Quadrature PSKの用語も使われています。Quadratureは「直角」以外に「方形」の意味もあるので「4個の」の解釈はできます。したがって、どちらでも正しいと思われます。
Quaternary PSK
Quadrature PSK
| 図 QPSKの出力波形 | 図 QAMの出力波形 |
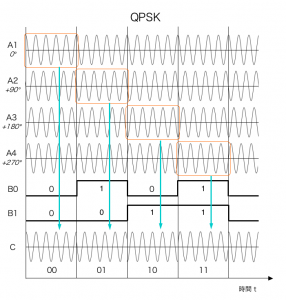 |
 |
多値変調のマッピング
次の図は、どこにデータを乗せるのか変調するときの信号の位置(コンステレーション・マップ Constellation Mapping)を表すものです。(時間軸で表示するオシロスコープの波形ではありません。)
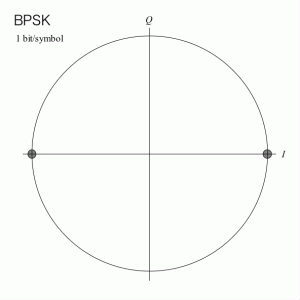
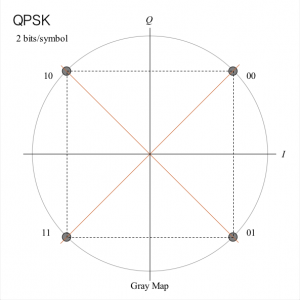
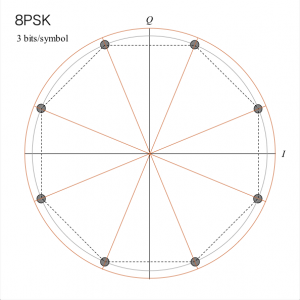
「位相変調」(PSK、Phase-Shift Keying)は、信号の位相情報(位相角、同心円は一つのみ)を利用しディジタルデータを乗せます。BPSK、QPSK、8PSKなどの種類があります。
| 図 BPSK | 図 QPSK |
 |
 |
| 図 8PSK | |
 |
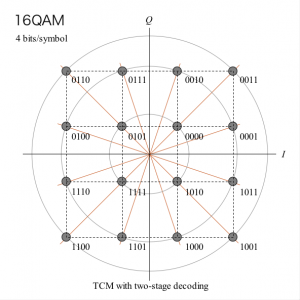
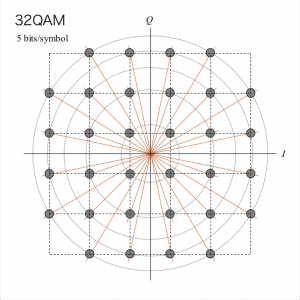
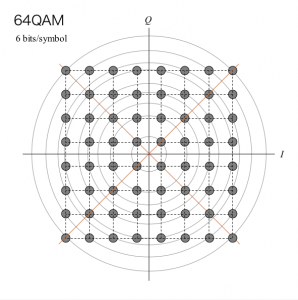
「QAM」(Quadrature Amplitude Modulation)は、振幅と位相の両方の情報(同心円は複数個)を利用します。傾きは、データを乗せる位相を表し、円の半径はデータの振幅を表します。16QAM、32QAM、64QAM、256QAMなどの種類があります。
図で「TCM」は、Trellis-Coded Modulation
| 図 16QAM | 図 32QAM |
 |
 |
| 図 64QAM | |
 |
ディジタル変調の帯域効率
次の表は、変調方式と帯域効率 (Spectral Efficiency) を比較します。理想的な状態では、帯域効率はシンボルレート(変調速度)に等しいですが、ノイズの影響により現実には達成できません。
- 帯域効率のたとえ話
- あまりうまい例えではありませんが、道路工事の砂利を積むトラックを想像してください。高いシンボルレートのトラックは荷台が大きく、それだけたくさんの砂利(信号)を積み込むことができます。トラックはがたがた道を走るうちに(ノイズで)揺れて砂利がこぼれます。
工事現場に着いたときには、砂利はこぼれて少し減った状態です。これは帯域効率に関係します。
送信側は設定したシンボルレートで送出しますが、伝送時にノイズでいくらかこぼれます。設定値に対して受信側がどれだけ受け取ることができるのか、帯域効率に関係します。
帯域効率が高いと一度にそれだけ多くのデータを伝送することができ、データレートは比例して上がります。
| 変調方式 | シンボルレート Symbol rate (bits/symbol) |
最大値 (組み合わせの数) | 帯域効率の理論値 Theoretical Spectral Efficiency(bits/sec/Hz) | |
| BPSK | 1 | 2 | 1 | |
| QPSK | 2 | 4 | 2 | |
| 8PSK | 3 | 8 | 3 | |
| 16QAM | 4 | 16 | 4 | |
| 32QAM | 5 | 32 | 5 | |
| 64QAM | 6 | 64 | 6 | |
| 256QAM | 8 | 256 | 8 |
- シンボルレート(≅帯域効率)と「表現できる値」の関係
- ・BPSKは最大値2で、1ビットを表現できる。(2の1乗=2)
・16QAMは最大値16で、4ビットを表現できる。(2の4乗=16)
・256QAMは最大値256で、8ビットを表現できる。(2の8乗=256)
ノイズの影響については、BPSKを例にとると、帯域効率の理論(上限)値は1ビット/秒/Hzです。この値は上限値であり、ごく至近距離の伝送ならともかく、現実にはノイズの影響により達成できないと考えるのが理にかなっています。実際にほとんど達成できず、値は減少します。
帯域効率とノイズ
シンボルレートを上げると帯域効率も上がりますが、無条件にいくらでも上げることはできません。変調方式「QAM」の図を参照すると分かりますが、nの数値は大きくなるにつれて、データと別のデータの間隔は狭まります。つまり、ノイズの影響を受けやすいことを意味します。
では、送信パワーを上げるとどうでしょうか?
確かにこれも一つの解で、送信パワーを上げるとデータとデータの間隔は広がります。しかし、やたらに送信電力を上げると周囲に影響を及ぼします。現実には電波法の規定があり制限を受けます。
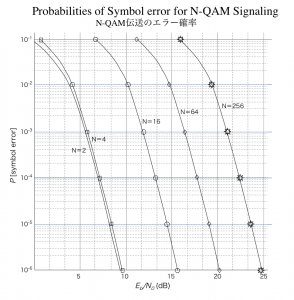
次の図は「N-QAM変調」を例にとり、特性について説明します。
文献(*1)から引用した図です。
図 N-QAM伝送のエラー確率
| 項目 | 説明 | |
| 縦軸は、エラーの確率 | 10-1=1/10、10-2=1/100、肩の(-)付きの数字が増えるごとに1/10の比率で小さくなる。 | |
| 横軸は、信号対雑音比の一種 | グラフの右に行くほどノイズの影響を受ける。 | |
| dB | デシベル 常用対数で大きさを表現する方法。信号とノイズ強度は電力を表し、電力では、10×log10(P)の計算。 | |
| Eb Bit energy | (信号)ビット強度 | |
| N0 Noise power spectral density | ノイズ電力スペクトル密度 |
図において、同じエラーの確率(横の一直線)の条件を比較します。1/10の確率 (10-1) のときN=4とN=256では15dBの違いがあります。
つまり、256QAMは4QAMと比べると、それだけノイズの影響を受けやすいことが分かります。帯域効率を稼いで、一度に伝送できるデータ量を多くできる代わりに、ノイズの影響を受けやすいのは、信号と信号の間隔が狭いので当然の結果であり、トレードオフです。
参考資料
*1 A First Course in Digital Communications
Hah. Nguyen、Ed Shwedyk共著 Cambridge University Press 2009年