同軸ケーブルとノイズ

＜更新情報＞
2014年2月8日
記事の最後に近い部分で、「20dB/decade=6dB/octave」が成立する理由を追加しました。

2014年1月27日
図3.3に誤りがあり、入れ替えました。「相互コンダクタンス　Mutual inductance」の表記は誤りで、正しくは「相互インダクタンス　Mutual inductance」です。訂正します。
なお、この図とは無関係ですが、「相互コンダクタンス　transconductance」は真空管やFET (Field Effect Transistor) などの素子において、電流を制御するパラメータで増幅率に関係します。

2014年1月12日
図4.3で、相互インダクタンスの記号に誤りがあり入れ替えました。

───────────────────────────────────

1. ノイズとシールド

電子回路やこれを使用する装置においては、ノイズの影響を可能な限り少なくすることはとても重要です。といっても、ノイズレベルをどこまで下げる必要があるのかは、システムの要求仕様によりさまざまです。一般の装置はそれほどでもありませんが、低ノイズを要求する計測器などにおいては桁違いの性能が必要です。

ノイズに関するテーマはいくつもありますが、ここで問題にするのは外来ノイズで、しゃへい（遮蔽、シールド　shield）は外来ノイズを防ぐものです。外来ノイズの低減方法について、系統立てて解説する資料はあまり多くありません。ノイズについて解説しようとすると非常に広い範囲のテーマに触れなければならずなかなか大変です。

この記事は、ノイズの低減に関するものではなく、同軸ケーブルのシールドの効果に焦点を当てたものです。同軸ケーブルに限らず一般のシールドの効果に関して十分に説明しようとすると、こちらも非常に広い範囲にわたり、少なくとも次の項目に触れる必要があります。この記事では関連する事柄について省略する部分が多く、また機会をみて解説します。

: ・容量結合　capacitive coupling
・誘導結合　inductive coupling
・近傍電磁界　near field
・遠方電磁界　far field
・波動インピーダンス　wave impedance
・材料のシールド効果
　　吸収損失　absorption loss
　　反射損失　reflection loss

2. 同軸ケーブルのシールド効果

同軸ケーブルは、極めて重要な特性を備えます。

それは、「電磁シールド」の効果も合わせて備えるのです。

同軸ケーブルの構造は、中心導体を外側の導体が覆うことにより「静電シールド」の効果は元から備わっています。

2.1 静電シールド

「静電シールド」は、二つの導体間の静電結合 (electrostatic coupling) 、または容量結合 (capacitive coupling)をさえぎる役目をするしゃへいのことです。別のいい方をすると電界 (electric field strength) をさえぎる働きをします。電界は電荷 (electric charge) に力を及ぼす性質です。

二つの導体間には、静電容量 (capacity) が存在します。導体の間には例外なく存在し、ノイズは侵入経路の一つである静電結合をとおして容易に通り抜けます。

: キャパシタ (capacitor)は、静電容量を積極的に利用する代表的な部品です。（日本語ではコンデンサの言い方がありますが、condenser は capacitorとは異なる別の機能を有する装置や部品のことであり明確に区別します。）; タッチ・センサ (touch sensor) には、静電容量を利用するものがあります。センサにつないだ電極は人体との間に生じる微少な容量の変化を検出し、コントローラで制御することにより機械的なスイッチの代わりを実現できます。（静電容量ではない仕組みのものもあります。）

「遮音」や「遮光」は、字のとおり音や光をさえぎることにより目的を達します。静電シールドもこれと似たところがあります。異なる点は、静電シールドは網目状の板、つまり小さな穴があっても十分に働く点です。

ただし、直流 (f=0Hz) や低周波の場合は、大きな編み目でも静電シールドは十分に機能しますが、高周波では編み目の大きさが問題です。電界もそうですが、磁界の漏れも大きな問題です。

同軸ケーブルの外側に位置するシールドは、中心導体を流れる電流の帰路であり、静電シールドも兼ねる働きをします。

静電シールドは簡単に実現でき、原理は単純です。しゃへいする電界の電圧をほぼ 0に近い値にすることができます。

静電シールド　electrostatic shield: 別名は、ファラデーシールド　Faraday shield
（Faradayはイギリスの物理学者）

図2.1　静電シールド

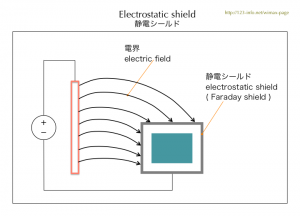シールドの中にあるものは電界の影響をほとんど受けません。

「電界」を雷に置き換えても同じです。電流はタイヤを通じて地面に伝わり、自動車の中の人は安全です。車のタイヤは機械的強度を増すカーボンブラック（炭素の微粒子）を混入したゴムで作られ電流を良く伝えます。電気コードなどの絶縁体に用いる天然ゴムとは異なる特性です。

3. 同軸ケーブルの誘導結合

同軸ケーブルに備わる電磁シールドの効果は、その構造に由来します。なぜ、そのような効果があるのか、理解するにはまず特性を知ることが必要です。

ツイストペア・ケーブルは２本のワイアをひねった構造で、通過する磁界を打ち消す効果があります。同軸ケーブルの構造はこれとは異なりますが、同じ効果があります。

解説記事: 伝送路とは [5]　ーツイストペア・ケーブル

同軸ケーブルのシールドと中心導体のそれぞれには自己インダクタンスが存在し、二つの導体間には相互インダクタンスが働きます。

ケーブルの外側にあるシールドに電流を流すと、ファラデーの電磁誘導の法則 (Faraday’s law of induction) により周囲には磁界を誘起し、相互インダクタンスの影響により中心導体には起電力を生じます。

インダクタンス　inductance

電流 I は、これに比例する磁束φを誘起します。インダクタンス L はこの比例定数のことです。L に流れる電流は電圧を発生します。インダクタンスは、一般に電流 I により電圧 V を誘導する性質で知られます。ワイアを巻いたコイル（coil、インダクタ　inductor）はインダクタンスの性質を有する代表的な部品です。

インダクタンスは、何も仕掛けのない直線状のワイアにも存在します。電流は磁束を生じるからです。大きさは1ミリメートルあたり約 1nH です。コイル状にグルグル巻くと増大します。

鉄などの高い透磁率の材料に巻いたコイルは大きなインダクタンスを得ることができます。ただし、いいことばかりではなく、損失や飽和などの致命的な欠点を生じる代償との引き換えです。

同軸ケーブルでは、ワイアのインダクタンスが誘導結合による電磁シールドの効果をもたらしますが、多くの回路においては配線のインダクタンスは厄介で邪魔な存在であり、トラブルの種です。

自己インダクタンス　self inductance

「自己インダクタンス」は、電流 I の変化により生じる電圧 V が同一の物体に起こる性質を表します。要するに「自身のインダクタンス」のことです。

相互インダクタンス　mutual inductance

インダクタンスを有する二つの部品の間に存在する性質です。「相互インダクタンス」は、電流 I の変化により生じる電圧 V が相手側に発生する性質を表します。相互インダクタンスは、単独では発生しません。

図3.1　同軸ケーブルの誘導結合
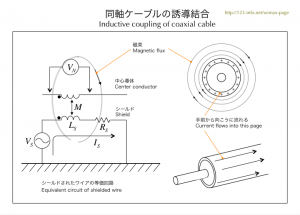同軸ケーブルの誘導結合　Inductive coupling of coaxial cable	R_Sはシールド・ワイアの抵抗成分です。インダクタンスや抵抗成分などは、集中定数 (lumped constant) により単純化して表します。

3.1 中心導体に誘起する電圧

シールドを流れる電流は中心導体に電圧を誘起します。この特性は周波数により変化します。

同軸ケーブルのこの効果は、低い周波数では十分ではなく、以下に示す周波数より上では効果を発揮します。

低域の周波数では「同軸」はただその形状だけであり、中心導体に誘起する電圧の効果は下がります。低域では、同軸ではないただの2本のワイアと同じ働きしかありません。

この周波数のことを「しゃへい遮断周波数」や「臨界周波数」 (shield cutoff frequency または shield break frequency) （以下 f_s）といいます。[1a, 1b, 2, 3, 5]

中心導体に生じる起電力は次の式で表すことができます。
　　 $V_N= j\omega M I_S$ 　　(3.1)

図3.1より
　　 $I_S= \frac {V_S} {j\omega L_S + R_S}$ 　　(3.2)

分母と分子をL_Sで割ると次の式に変形できます。
　　 $I_S= \frac {V_S} {L_S} \left( \frac {1} {j\omega + R_S / L_S} \right)$ 　　(3.3)

式(3.3)を(3.1)に代入すると
　　 $V_N= \left( \frac {j\omega M V_S} {L_S} \right) \left( \frac {1} {j\omega + R_S / L_S} \right)$ 　　(3.4)

ここで、シールドの自己インダクタンスは次の式で表すことができます。
　　 $L_S= \frac {\phi} {I_S}$ 　　(3.5)

また、シールドと中心導体との間の相互インダクタンスは次の式で表すことができます。
　　 $M= \frac {\phi} {I_S}$ 　　(3.6)

シールドを流れる電流が誘起する磁束は中心導体を取り囲むので、式(3.5) と (3.6)の磁束は等しいことから次の式が成立します。
　　 $L_S= M$ 　　(3.7)

式(3.4)に(3.7)を代入し、次の式に変形します。
　　 $V_N= V_S \frac {j\omega} {j\omega + R_S / L_S}$ 　　(3.8)

式(3.8)が示すのは、シールド電流の影響により中心導体に発生する電圧の周波数特性です。次の図に示します。電磁シールドの効果は、この特性と密接に関係します。

図3.2　しゃへい遮断周波数
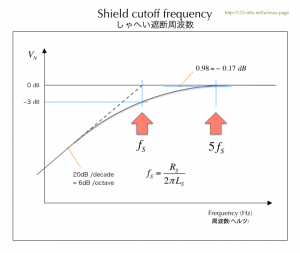しゃへい遮断周波数　Shield cutoff frequency	シールドに電流を流すと、相互インダクタンスにより中心導体には電圧を誘起します。f_sより低い周波数ではシールドの影響が十分ではないことが分かります。縦軸の値は5f_sで0.98に達し、同軸ケーブルが電磁シールドの効果を十分に発揮する周波数はこれより上の領域です。

f_sの具体例です。[1a, 1b, 2, 3]

ケーブル	特性インピーダンス Zo	f_s	5 f_s
RG-58C	50Ω	2KHz	10KHz
RG-59C	75Ω	1.6KHz	8KHz

3.2 中心導体とシールドを流れる電流

同軸ケーブルには、図3.2と密接に関わるもう一つの重要な性質があります。

次の図の回路で、中心導体を流れる電流は負荷抵抗 R_Lに達すると、条件によりシールド・ワイアまたはグランドを帰路に流れ信号源に戻ります。

5 f_S以上では中心導体とシールド・ワイアの二つの電流はほぼ等しいことを説明できます。[1a, 1b, 2, 3, 5]　この意味するところは、5 f_S以上では信号電流の帰路はグランドを通らずに、シールドワイアだけを流れる非常に興味深い点です。

図3.3　シールドとグランド電流
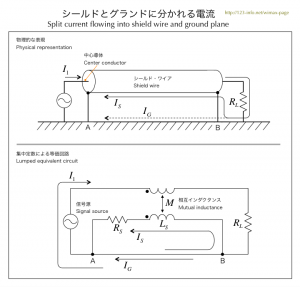シールドとグランド電流　Shield and ground current	信号電流の帰路は、直流ではグランドのみを流れます。周波数が上がるにつれ序々にシールド・ワイアの電流は増加し、5 f_Sより高い周波数においてはほぼシールド・ワイアのみを流れます。

以上を数式で説明します。

グランド・ループ ( B – L_S – R_S – A – B )を流れる電流は
　　 $0= I_S \left( j\omega L_S + R_S \right) - j\omega M I_1$ 　　(3.9)

式(3.9)を変形すると
　　 $I_S= I_1\left( \frac {j\omega} {j\omega + R_S / L_S} \right) = I_1 \left( \frac {j\omega} {j\omega + \omega_C} \right)$ 　　(3.10)

式から分かることは、5 f_S以上の周波数では、式(3.8)のかっこのなかは 1に漸近し、I_S=I₁が成立します。これは、中心導体を流れる信号電流の帰路はグランドを通らずに、シールド・ワイアだけを流れることを意味します。

非常に興味深いことに、この現象はグランドの抵抗値がたとえ 0でも成立します。

それは、なぜか？

同軸ケーブルは、電流が流れると中心導体とシールド・ワイア間に発生する相互インダクタンスの作用を生じますが、ちょうどコモンモードチョークのように働くのがその理由です。[2, 3]

図3.4　コモンモード・チョーク
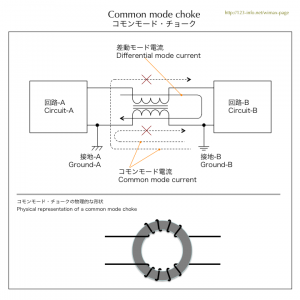コモンモード・チョーク　Common mode choke	コモンモード・チョークは、図のように差動モード信号 (differential mode signal) のみを通し、同相モード信号 (common mode signal)を通さない作用があります。また、グランド-Aとグランド-Bを分離する作用もあります。

差動モードと同相モード

どんな機器でもある程度のノイズが乗ることは避けられません。たとえば、AC電力ラインは日本では100Vですが、さまざまな機器が発生するノイズで溢れており、電気的にクリーンであるとはとても言えません。発電機が生成する電力は割ときれいな正弦波状の波形ですが、雷などの自然現象もあります。電力会社は管理の目的で微少信号を重畳しますが、オシロスコープで観測するとノイズに見えるかもしれません。それよりも、どこかの家庭で使用する家電製品から発生するもっと大きなノイズはACラインを伝わりやって来ます。特に、ミキサーや掃除機などの整流子モーターは盛大にノイズを発生します。

高効率で感度の高いスピーカーから電源オフのときに、スピーカーコードが拾うノイズが聞こえることがあります。ごく上等のオーディオ装置から最上の音を引き出そうとする熱心な人は、ACラインのノイズを防ぐことに神経を尖らせることでしょう。

外来ノイズは二本の線の間に現れるだけではありません。非常に厄介な問題があります。ワイアに現れるノイズには二種類あり、差動モードと同相モードがそれです。

差動モード・ノイズは二線間に入るもので、二線間だけに作用する普通のライン・フィルタは効力を発揮します。しかし、同相モードノイズはこのフィルタを何段重ねようがまったく取れません。

同相モードノイズはいわば仮想のグランド基準があり、二本の線に同等に重畳します。たとえると、装置に相当する船全体がノイズの波間に揺れるようなものです。したがって、普通のノイズフィルタはまったく役に立ちません。同相モードノイズにはコモンモード・チョークは有効です。

最近の電子機器の電源装置は、スイッチング・レギュレータ (switching regulator, SMPS: Switch Mode Power Supply)の割合が増加していますが、スイッチングの作用により電力を変換・生成します。矩形波（台形波）による典型的な仕組みの回路は、その原理からスイッチングノイズの発生を免れることはできません。その成分には同相モードノイズがあり、コモンモード・チョークは非常に有効に作用します。

4. 電磁シールドの原理と効果

同軸ケーブルに備わる電磁シールドの特性は、すでに触れたようにその構造に由来する本質的なものです。

同軸ケーブルにはなぜ電磁シールドの効果があるのか？

原理は単純です。

ファラデーの電磁誘導の法則が示す物理です。法則はどのように働くのか、これは、ケーブルの中心導体とシールド、二つのワイア間に存在する相互インダクタンスに働きます。

仕組みは非常に単純なゆえに見過ごしてしまう現象です。しかし、解析するのはなかなかめんどうです。このテーマに触れる文献は、知る限りではごくわずかしかありません。ここでは、外部信号の誘導による同軸ケーブルに発生する信号の大きさを解析し、効果を検証します。

信号はジェネレータ・ワイアから発生します。図中にあるレセプタ・ワイア（ここでは中心導体を指します。「レセプタ　receptor」は受けるもの＝受容器の意味）に誘導する信号がどれほどの大きさなのかは注目に値します。

ここに示す等価回路はかなり単純化したもので、実際にははるかに複雑と考えられます。単純化の一つは、図では集中定数回路で示してある点で、高い周波数で考えることには無理を生じます。

集中定数回路　lumped constant circuit: 平たくいうと、波長の長さを無視できる回路です。分布定数回路 (distributed constant circuit) は、これに対比します。一般には低周波を扱う回路は、集中定数で扱うことができます。ただし、もう使われなくなりつつあります（日本では、幹線の電話網は光ファイバによるディジタル回線ですが、アナログ回線はわずかに電話局から加入者宅までの数Kmです。）が、長大な電話網は波長を無視することができないので分布定数回路の扱いです。配線長が1/6〜1/8波長を超えるあたりから分布定数回路を意識することが必要です。

次の図は、ジェネレータ・ワイアと同軸ケーブルの位置関係を示します。

図4.1　同軸ケーブルと誘導電流
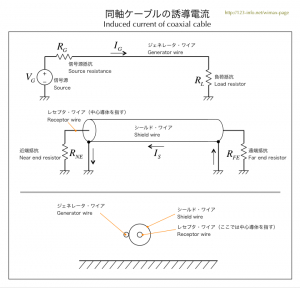同軸ケーブルと誘導電流　Induced current of coaxial cable	実験結果を紹介する予定ですが、二本のワイアの位置は図のようにほとんど密着した状態です。

図4.2　誘導結合の集中定数等価回路
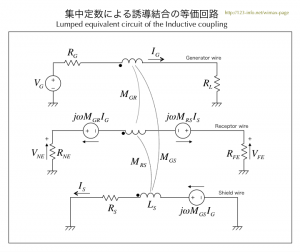誘導結合の集中定数等価回路　Lumped equivalent circuit of Inductive coupling	3本のワイアの間にはそれぞれ相互インダクタンスが作用します

4.1 同軸ケーブルと電磁誘導

同軸ケーブルの外側に置いたジェネレータ・ワイアに電流 I_G を流すと、ファラデーの電磁誘導の法則により、レセプタ・ワイア（ここでは中心導体）とシールドにはそれぞれI_G と逆向きの電流を誘導し、起電力を発生します。[4]

レセプタ・ワイアからグランドのループに発生する起電力は、 jωM_GR I_Gで、シールドからグランドのループに発生するのは jωM_GS I_Gです。

起電力

「起電力」は、電流を流せる電位差のことで、具体的には「電圧源　voltage source」です。

たとえば jωM_GRは抵抗値を表し、I_Gは電流ですから、オームの法則より抵抗×電流は電圧を表すことが分かります。

シールドに誘起する電流 I_Sは、オームの法則から次のように表すことができます。
　　 $I_S= I_G \left( \frac { j\omega M_{GS}} {R_S + j\omega L_S} \right)$ 　　(4.1)

右辺のかっこのなかの分子は、ω (=2π f) と相互インダクタンスM_GSの積で形成するインピーダンスで、分母は、純抵抗R_Sと、分子と同様に自己インダクタンスL_Sのインピーダンス (ωL_S)の和による分圧比を表します。これにI_Gをかけ算した値はI_Sと等しいことをこの式は示します。

インピーダンス

初心者の方向けに：
jω Ls の意味は、インダクタンスの抵抗値は周波数により変化するからです。これを「インピーダンス」と言い表します。jωがあるので難しく感じるかもしれませんが、この表現は避けられません。

純抵抗は周波数を変えても値は変化しませんから、jωは付きません。

数学の世界では虚数は i で表現しますが、電気の世界では電流 I (Intensity of current) の記号と混同しやすいので代わりに j を使います。ここで示す式は、すべて初歩的なものばかりです。

完全な「純抵抗」は現実には存在しません。回路図では好きなだけ理想部品を書くことはできます。時にはそれらが理想ではない事から来る影響を可能な限り避けることが求められ、非常に困難なことがあります。

シールドに誘起する電流 I_Sは副次的な効果を発生し、レセプタ・ワイアからグランドのループに I_Sとは逆向きの電流を誘導し起電力を生じます。

二次効果により発生する起電力は、jωM_RS I_Sです。

: M_RSは、レセプタ・ワイアとシールド間の相互インダクタンス

ニア・エンド側の抵抗R_NEに生じる起電力は
　　 $V_{NE}= j\omega \left( \frac{R_{NE}} {R_{FE} + R_{NE}} \right) ( M_{GR} I_G - M_{RS} I_S )$ 　(4.2)

式(4.2)は、(4.1)を代入し次のように変形できます。
　　 $V_{NE}= I_G \left( \frac{R_{NE}} {R_{FE} + R_{NE}} \right) \left( \frac {j\omega R_S M_{GR} + \omega^2 (M_{GS}M_{RS} - M_{GR} L_S)} {R_S+j\omega L_S} \right)$ 　(4.3)

理由の説明は省略しますが、次の式が成立します。[4]
　　 $M_{GS}=M_{GR}$ 　(4.4)

さらに、次の式も成り立ちます。[1a, 1b, 2, 3]　こちらは、式 (3.7)とまったく同じです。
　　 $M_{RS}=L_S$ 　(4.5)

(4.3)式は、(4.4)と(4.5)の二つを適用し置き換えると次のように書くことができます。（M_GSとM_RSを置き換えると ω²() の項は消去できる。）
　　 $V_{NE}= j\omega M_{GR}I_G \left( \frac{R_{NE}} {R_{FE} + R_{NE}} \right) \left( \frac{R_S} {R_S + j\omega L_S} \right)$ 　　(4.6a)

さらに、V_FEについては(4.6a)式のR_NEをR_FEに置き換えて次のように書けます。
　　 $V_{FE}=-j\omega M_{GR}I_G \left( \frac{R_{FE}} {R_{FE} + R_{NE}} \right) \left( \frac{R_S} {R_S + j\omega L_S} \right)$ 　　(4.6b)

ここで、I_Gは図4.2の等価回路からオームの法則により
　　 $I_G=\frac{V_S} {R_S + R_L}$ 　　(4.6c)

(4.6a)と(4.6b)の二つの式において、最初の二つの係数はレセプタ・ワイア（中心導体）に発生する電圧を表し、シールドがないときのクロストークです。つまり、シールドのない条件では、この大きさそのままの電圧が現れます。（最初の係数は「抵抗×電流＝電圧」を表し、二つ目の係数は抵抗分割の比率を表す。）

三番目の係数は、シールドの抵抗成分とインピーダンスから成る抵抗分割の比率で、シールドの効果を表します。

係数の説明は、どれが何番目なのか文章だけでは分かりにくいので、図解します。それぞれの係数がどんな意味を表すのかは、上記のとおりです。

図4.3　クロストークとシールドの効果
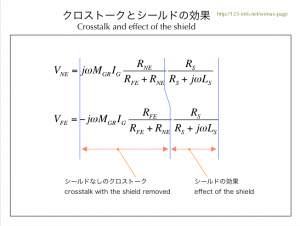クロストークとシールドの効果　Crosstalk and effect of the shield	「クロストーク　crosstalk」は一つのワイアなどの部品や回路ブロック等から他の部分に漏れる信号のこと。ここでは、ジェネレータ・ワイアからレセプター・ワイアに漏れる信号。

シールド効果係数 SF (Shielding Factor)のみを抜き出すと
　　 $SF=\frac{R_S} {R_S + j\omega L_S}$ 　　(4.7)

シールド効果係数 SFの項は、文字どおりシールド効果の周波数特性を表し、次の式に変形できます。
　　 $SF=\frac{1} {1 + j (f / f_S)}$ 　　(4.8)

ここで、f_Sはしゃへい遮断周波数で、図3.2に示したものと等しい値です。
　　 $f_S=\frac{R_S} {2\pi L_S}$ 　　(4.9)

シールド効果係数 SFは、次のように近似することができます。
　　 $SF\simeq\left\{\begin{array} {ll}~~1 & for ~ (f < f_S)\\ \frac {R_S} {j\omega L_S} & for ~ (f_S < f) \end{array} \right.$ 　　(4.10)

シールド効果係数 SFをグラフにすると、図3.2と同じ特性を得られます。グラフの示す値を式で表現したものです。

4.2 誘導結合による計算結果のまとめ

式(4.6c)に示すI_Gと、(4.7)に示すSFの式を(4.6a)と(4.6b)にそれぞれ代入し、シールドのあるなしの場合分けを行います。

図4.4　クロストークとシールドの効果
クロストークとシールドの効果　Crosstalk and effect of the shield

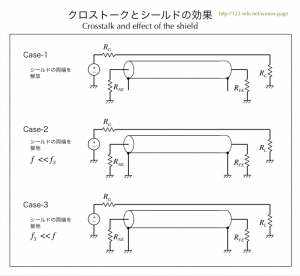ケース1　両端でシールドをグランドに接続しないとき
(4.7)式の”シールド効果係数 SF=1″ つまり、シールドがない（実際には存在するが、電気的にはないのと同じ）場合です。

　　 $V_{NE} = j\omega V_S \left( \frac{ R_{NE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right)$ 　　(4.11a)
　　 $V_{FE} = - j\omega V_S \left( \frac{ R_{FE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right)$ 　　(4.11b)

: シールドをグランドに接続しない条件では、シールド電流は流れません。したがって、ジェネレータ・ワイアを流れる電流 I_Gが発生する磁界を打ち消すことができません。

ケース2　両端でシールドをグランドに接続し、f << fsの条件　　　　（しゃへい遮断周波数より十分に低いとき）

　　 $V_{NE} = j\omega V_S \left( \frac{ R_{NE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right)$ 　　(4.12a)
　　 $V_{FE} = -j\omega V_S \left( \frac{ R_{FE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right)$ 　　(4.12b)

: 二つの式の番号を変えましたが、この条件では、ケース1とそれぞれまったく同じ式です。(4.7)式の”シールド効果係数”は SF=1の条件です。

ケース3　両端でシールドをグランドに接続し、fs << fの条件　　　　（しゃへい遮断周波数より十分に高いとき）

　　 $V_{NE} = V_S \left( \frac{ R_{NE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right) \left( \frac {R_S} {L_S} \right)$ 　　(4.13a)
　　 $V_{NE} = -V_S \left( \frac{ R_{FE} } { R_{FE} + R_{NE} } \right) \left( \frac{ M_{GR} } { R_S + R_L } \right) \left( \frac {R_S} {L_S} \right)$ 　　(4.13b)

: シールドの両端をグランドに接続する条件では、(4.7)式の”シールド効果係数”の分母は、jωL_SはR_Sより大きくなり、R_Sは無視できます。分子と分母のjωは消えL_Sだけが残ります。; この条件では、シールド電流I_Sは流れます。I_Sは、ジェネレータ・ワイアの電流 I_Gとは逆向きで、 I_Gが発生する磁界を打ち消す（正確には、完全に打ち消すのではなく弱める）効果を表します。二つの式が表すように、クロストークは周波数によらず一定であることが分かります。（あくまで、等価回路の条件で計算した結果です。実際には、単純な等価回路に現れない影響があることは十分に考えられます。）

誘導結合の影響を解析した結果は以上のとおりです。

5. 容量結合の影響を組み合わせる

クロストークの侵入経路は誘導結合だけではなく、また容量結合だけでもありません。両方の効果を考慮する必要があります。

非常におおまかな近似計算では、次に示すように、シールドの片方を接地すると容量結合の影響はほとんど無視できることがわかります。この場合の容量結合は、厳密には 0 ではありませんが、実用上はほとんど問題ないでしょう。

誘導結合と容量結合の両方によるクロストークは、次の式で表すことができます。
　　 $\frac {V_{NE}} {V_S} = \frac {V^{IND}_{NE}} {V_S} + \frac {V^{CAP}_{NE}} {V_S}$ 　(5.1a)
　　 $\frac {V_{FE}} {V_S} = \frac {V^{IND}_{FE}} {V_S} + \frac {V^{CAP}_{FE}} {V_S}$ 　(5.1b)

グラフにすると次の図で表すことができます。シールドの両端を接地した条件は、たて軸の値は別にして4.1項の最後に記したシールド効果係数 SFのグラフと同一です。

図5.1　誘導結合とシールド接地の効果
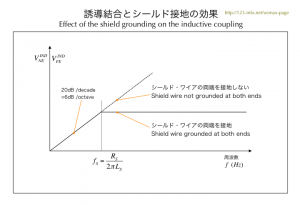誘導結合とシールド接地の効果　Effect of the shield grounding on the inductive coupling	レセプタ・ワイアに生じるクロストークは、f_sを境に特性は図のように変化します。

「20dB/decade」は、周波数10倍ごとに10倍の値に変化します。また、「20dB/decade=6dB/octave」が成立します。
20dBは電圧比では10倍を表し、「decade」は、ここでは10倍の周波数のことです。6dBは電圧比では約2倍を表します。

その理由は、それぞれ10と2の対数をとり比率を計算すると
（ここでは7桁の有効数字で計算しましたが、日常の現場では3桁もあれば十分です。）

\log_{10}10 \div \log_{10}2 \approx 1 \div 0.3010299 \approx 3.321929

6.020599dB（6dBより正確な2倍に近い値）にこの比率をかけ算すると、ほぼ20に一致することが分かります。

3.321929 \times 6.020599 \approx 20.0000

（あまり分かりやすい説明ではないかもしれません。）

「octave　オクターブ」はピアノの鍵盤では「ド・レ・ミ・ファ・ソ・ラ・シ」の範囲を表しますが、次の「ド」までを周波数で表すとちょうど2倍です。鍵盤の特定の「ド」から次の「ド」までは、周波数は2倍または1/2の関係です。

5.2 誘導結合の実験結果

実験結果を紹介したいと思いますが、次の機会にします。

参考資料: 1a　実践ノイズ逓減技法
松井　孚夫　訳　1978年　ジャテック出版　刊; 1b　1aの原著　Noise Reduction Techniques in Electronic Systems
H. W. Ott　著　1976年　John Wiley & Sons Inc.　刊; 2　Noise Reduction Techniques in Electronic Systems 2nd Edition
H. W. Ott　著　1988年　John Wiley & Sons Inc.　刊; 3　Elecrtomagnetic Compatibility Engineering
H. W. Ott　著　2009年　John Wiley & Sons Inc.　刊; 4　Introduction to Elecrtomagnetic Compatibility Second edition
C. R. Paul　著　2006年　John Wiley & Sons Inc.　刊; 5　解析ノイズ・メカニズム
岡村　廸夫　著　1987年　CQ出版社　刊