＜更新情報＞

2013年2月23日

タイトルに概要を追加しました。
「伝送線路のモデル（等価回路）」に説明を追加し、図も入れ替えました。

2013年2月20日

台形波の周波数スペクトルの説明について、t_r＝1nsの条件で説明しましたが、100psに修正します。かなり速い信号ですが、図の(1/πt_r)＝5GHzを満足する条件です。

t_r＝100pはUSB3.0の波形（600ps程度）等と比較するとまだ速い信号です。もう少し現実的に考えると、基本波＝10MHz、t_r＝1nsの条件で50倍＝500MHzです。（この場合は、「5GHz」を「500MHz」に読み替えてください。）

2013年2月20日

参考資料[8]の記載漏れがあり追加しました。

この記事は「伝送路の仕組み［２］ー 電流とは何？（電流の性質）」の続きです。

目次

・反射と吸収
・分布定数回路と特性インピーダンス
・伝送線路のモデル（等価回路）
・周波数、波長、配線
・矩形波と高速回路、高周波回路

反射と吸収

送信出力から出発した信号は、ケーブルまたはその他で構成した伝送路を伝わり受信入力に到達します。

送信出力と受信入力

・送信出力を「送信端　sending-end」とか「送端」と言い表します。
・受信入力を「受信端　receiving-end」とか「受端」と言い表します。

進行波　progressive wave

送端から受端へ向かう信号波のこと

反射波　reflected wave

受端から送端へ戻る信号波のこと

受端では、信号は常にすべて吸い込まれる訳ではなく、時には送端方向に戻る反射波が存在します。この現象が「反射　reflection」です。

反射の起こる条件があります。それは、後で説明する「特性インピーダンス」と送端または受端のインピーダンスが合わないからです。この状態を「不整合　mismatch」と言います。

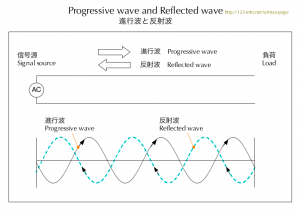
なぜ反射するのか、また、反射しないときの状態については、

1　受端で、何も吸収しないと他に行き場がない。元に戻るしかなく、反射して送端へ戻る。エネルギー保存の物理法則により、行き場のない信号は受端で消滅しない。行き場がないと元へ戻るしかない。

2　やってきた信号エネルギーを、受端で完全に吸収すると、反射しない。それ以上は何も起きない。

反射により「定在波（または定常波）standing wave」と呼ぶ現象が発生します。定在波は波が移動せずにその場で振動するように見える現象です。

定在波の画像

次のサイトには定在波のアニメーションがあり、分かりやすいかもしれません。
http://ja.wikipedia.org/wiki/%E5%AE%9A%E5%B8%B8%E6%B3%A2

定在波の比率、調整

反射波と進行波の大きさ（振幅）の比率を「定在波比　SWR　Standing Wave Ratio」と言います。SWRは電圧で扱うことが多く、これを「電圧定在波比　VSWR　Voltage Standing Wave Ratio」で表現します。

SWRを最小にして反射波を最小の状態にする方法は、具体的には後で説明する特性インピーダンスと送端または受端のインピーダンスを整合します。（現実には、反射0は達成できません。）

無線送信機では、SWRを最小にするように調整することが大切です。この状態にすると、送信機の出力を最大限に電波のエネルギーに変換できます。

分布定数回路と特性インピーダンス

なにやら難しそうな言葉をいきなり二つも出しました。次はその説明です。さらにもう一つあります。

「反射と吸収」のところで「特性インピーダンス」について触れました。ここでは、これについて解説します。

「特性インピーダンス」は、「分布定数回路」の性質を表します。

インピーダンス　impedance

「インピーダンス」は交流 (alternating-current) 信号を扱うときに、簡単に表現すると電流の通りにくさ＝交流抵抗」のことです。交流の特徴は周波数 (frequency) を伴うことです。

特性インピーダンス　characteristic impedance

この言葉だけでは知らない方には何のことか分からないと思います。「特性インピーダンス」は「分布定数回路」が有する回路の特性の一つで、伝送線路では重要なパラメータです。特性インピーダンスは、モデル化したパラメータにより表現します。具体的には下の説明と図を参照してください。

分布定数回路　distributed constant circuit

分布定数回路は、「高周波信号」や「高速・広帯域の信号」を扱う回路では避けて通れません。この回路の特徴を簡単に表現すると、信号を伝えるときに時間を気にします。

もう少し正確に表現すると、信号を伝えるときに伝送路の長さと比べて信号の波長が十分に長いとみなせない伝送路では、伝達時間を無視することができません。（無視できるのは「集中定数回路」と言います。）「分布定数回路」は、信号の伝達に関わる回路の要素を分解してモデル化した回路のことです。

伝達時間を無視するとどんな問題があるのか、具体的には、つないだだけでは反射などの影響を受け、信号は正しく伝わりません。信号を正しく伝えるには正しい設計は欠かせません。

集中定数回路　lumped constant circut

「集中定数回路」は「分布定数回路」と対比します。ごく普通に扱う回路のことです。信号伝達に要する配線長の影響は無視できます。

たとえば、オーディオ信号を扱う回路はこれに相当します。

ディジタル・オーディオの信号は別で、それはすでにオーディオ（可聴帯域）信号ではありません。この記事で説明しているテーマはそのまま当てはまることがあります。

電気ワイアを使用する固定電話の回線はオーディオ帯域ですが例外で、分布定数回路の扱いです。しかし、現在ではアナログ回線は電話局までしか残っておらず、距離は短いので分布定数回路としての扱いは薄れていると思います。（電話網はほとんど光ディジタル回線です。また、電話局までも光回線の場合は、この記事のテーマには該当しません。）

伝送線路のモデル（等価回路）

「伝送線路」は、図のように回路を等価回路で表すことができます。[8]

図では限界があり、理想的なモデル化はできません。「LRGC」の素子をいくつか書けますが、理想モデルでは無限の数で表現します。つまり、無限に分割すると理想の回路モデルを表現できます。現実にはそんなことは不可能であり、回路シミュレーションでは有限個の数で行います。

伝送線路の特徴について、大変重要なことがあります。

「反射波」が存在しない理想の状態にすると、通過する信号にとって伝送線路は、じゃまなものが存在しない透明なパイプのように見えるという点です。しかし、現実には損失等があり、少し曇ったパイプにみえます。（ただし、「終端」の方法により伝送線路の振る舞いは異なります。「受端終端」で理想的な条件では、透明なパイプのように見えます。）

Telegrapherの式

特性インピーダンスは、図中の式により導きます。二つの式は微小距離 y に対する電流と電圧の変化を表すものです。

ここには興味深いことが含まれています。図中の上の式は微小距離 y に対する電流 i の変化率（偏微分）を表し、そこには電圧の変化（偏微分）が含まれています。つまり電圧が変化すると電流も変化することを意味します。下の式では、電流と電圧の関係が入れ替わります。このことが何を意味するのかです。

電波（電磁波）は電流を流したときに発生する磁界と、電圧をかけたときに発生する電界が交互に作用し空間を伝播する現象ですが、ワイアの周りに生成する同じ現象を空間に放出したものです。二つの式は電界と磁界が交互に発生する現象と密接に関係するものと考えられます。

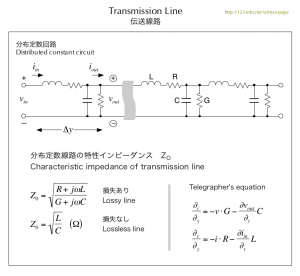
図で、理想のモデルではRとGはありませんが、現実の伝送線路では無視できません。RとGは損失を表し、小さいと損失も小さくなります。さらに、高い周波数では電流が導体の表層部のみを流れる現象「表皮効果　skin effect」があります。表皮効果はRを増大する方向に作用します。

回路のモデルは、マクスウェル (James Clerk Maxwell) の方程式を使って作り出されたものです。

周波数、波長、配線

「周波数」とは、振動数のことですが、電気の世界では「1秒間の振動数」で定義します。

では、ここで問題です。次の3種類の波形の周波数は、それぞれいくつでしょうか？

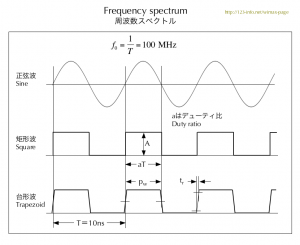
正弦波は簡単です。１周期よりf＝１/T＝100MHzです。

矩形波と台形波は、そうはいきません。

普通に「クロック周波数」のような言い方では、正弦波と同じ100MHzです。これは、波形のただ一つの特徴を表しただけに過ぎません。二つの波形には別の特徴があり、伝送線路を設計する上ではそちらのほうがはるかに重要です。

二つの波形は、それぞれたくさんの高調波を含むのですが、その答えは次の図[3]と、その次の図です。

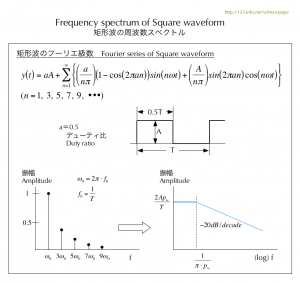
二つのグラフは何を意味するのか、周波数対振幅、つまり周波数スペクトルです。左はスペクトルごとの振幅、右は単純化して上側の包絡線のみを描いてあります。

グラフについて

−20dB/decade　10倍(decade)の周波数で、振幅は1/10(−20dB)に減衰
−40dB/decade　10倍(decade)の周波数で、振幅は1/100(−40dB)に減衰
　　
次は覚えておくと便利かもしれません。
−20dB/decade＝−6db/octave （2倍の周波数で1/2に減衰する）

時間軸で表す波形がなぜグラフの特性になるのかについて、これを一言で表現するならば、時間軸（タイムドメイン　time domain）の信号をフーリエ変換 (Fourier transform) すると周波数ドメイン (frequncy domain) の信号に姿を変えます。

「矩形波」は、理想的には図のように、「立ち上がり時間　rise time」＝0 の波形ですが、現実世界の現場で「矩形波」というときは、実際は台形波のことを意味する場合がほとんどです。（矩形波は理想波形の一種であり、現実には存在しません。なぜなら、立ち上がり時間0は無限大の周波数スペクトルを含みますが、こんなものは実現不可能です。）　　

したがって、理想波形の矩形波は検討の対象ではなく、ここでいう台形波が対象です。周波数スペクトルは次の図のように高い周波数の高調波を含みます。条件により異なりますが、一般に基本波（この例では100MHz）の50倍程度までの範囲を考慮の対象にします。（次の図で右側の折れ点の周波数）

その「波長」とは、基本波100MHzの矩形波（正確には台形波ですが）では、その50倍あたり5GHzです。この周波数ではエネルギーはかなり落ちますが、この付近まで考えなければならないということです。

次の図は、台形波の周波数スペクトルを表します。現実の波形は矩形波ではなく、台形波で高精度に近似することができます。[5]

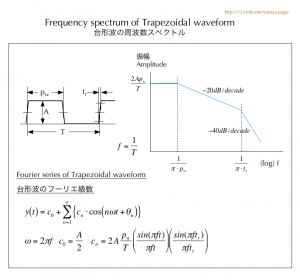
ディジタル回路では、矩形波（台形波）を扱いますが、だんだんと高速化する傾向にあります。「高速」とは、波形の立ち上がり時間を意味します。（間接的に処理速度の高速化にも結びつきます。）

矩形波（台形波）は、特に伝送距離が伸びると正しく設計した伝送線路でなければ意図したとおりの動作は得られないことがあります。こんなとき、配線長のどこまでが集中定数回路で良いか、いくら以上のときに分布定数回路として扱わなければならないのか、目安を知ることは重要です。

「伝送距離」のところで、ヒントの一つは「波長と配線長の比率」と書きました。「配線長が波長の1/100を超えるときは伝送線路として扱う[4]」という考え方があり、これも有効です。しかし、信号が正弦波の場合は簡単ですが、矩形波（台形波）ではどの周波数の高調波を選ぶのかという問題があり、簡単に計算できません。

波長との比率以外のもう一つの考え方は、立ち上がり時間から「有効電気長　EEL　effective electrical length」を計算する方法があります。[6] [7]

有効電気長の計算例

計算結果を紹介すると、tr＝1nsのとき
EEL＝6cm [文献6]
EEL＝5cm [文献7]

　　
この距離を超える配線長では、分布定数回路として設計しなければならないことを意味します。二つの文献の結果は異なりますが、これらの数値は目安です。

ここであげた例のような周波数を扱う回路は、想像以上に高い周波数の影響を受けることがお分かりでしょうか。

矩形波と高速回路、高周波回路

「高速回路」とか「広帯域回路」という言葉を聞くと思います。PCや携帯型の端末など情報処理装置は、処理の高速化に伴い動作速度もだんだんと高速化してきました。

さらに言いたいことは、実はもう書いていますが、「高速回路」＝「広帯域回路なのです。ここでは「高速」の意味は、信号電圧の変化率（単位時間あたりの振幅の変化率＝スルーレート　slew rate）を表します。

理論上の説明は、変化率大では短い時間で電圧は変化し、高い周波数成分を含むことは直感的にも分かると思います。実際に「台形波の周波数スペクトル」の図にある、t_rが小さい（変化率大）と、グラフの右側にある周波数は高いほうへ移動することが分かります。すなわち、「高速の変化」＝「周波数高」を意味し、台形波は直流成分を含むので、帯域幅は拡大します。

「周波数、波長、配線」のところで書いたように、基本波100MHzの矩形波（正確には台形波）を扱うときに考えなければならない周波数は、DC（直流 0Hz）から5GHzくらいまでの広い範囲です。5GHzと言えば、無線通信で扱う高周波回路と変わりません。

このように、対象にする矩形波（正確には台形波）の周波数スペクトルがどこまでの範囲なのかを考えることは、極めて重要な問題です。

次の記事「伝送路の仕組み［４］ー 同軸ケーブル」に続きます。

参考資料

[3]　EMCと基礎技術　　鈴木茂夫　箸　1999年　工学図書　刊

[4]　Handbook of Electronics Calculations
　　M. Kaufman, A. H. Seidman　箸　1979年　Macgraw-hill Book　刊

[5]　Bandwidth of Digital Waveforms　L. R. Paul　著　Mercer University (USA)　刊

[6]　Circuits, Interconnections, and Packaging for VLSI
　　H. B. bakoglu　箸　1990年　Addison-Wesley　刊

[7]　High Speed Digital Design 　A Handbook of Black Magic
　　H. W. Johnson, M. Graham　箸　1993年　Prentice-hall　刊

[8]　Transmission Line Handbook
　　B. C. Wadaell　箸　1991年　Artech House, Inc. 刊