───────────────────────────────────
＜更新情報＞
2014年11月2日
　　ADSLにおいて、電話局までの距離が長いとなぜ伝送容量が小さい（通信速度が遅い）のか説明を追加しました。
───────────────────────────────────

伝送路容量（通信路容量、伝送速度）とケーブル

有線通信ネットワークにおいて、伝送路容量（ビット毎秒、速度）はケーブルの距離により変化します。原因は、信号の減衰とノイズです。

身近で分かりやすい顕著な例は、DSL（ADSLなど）です。信号の送信と受信を行うモデムがたとえどんなに高性能でも、全体の性能はほぼ伝送路（通信路、channel）で決まります。

ADSLの伝送路容量（通信路容量、伝送速度）と距離

まだ64Kbpsモデムを使っていた頃、1996〜97年頃だったと思いますが、1Mbpsのモデムを開発中のニュースを知り、当時はとても驚きました。今でこそADSLは当たり前ですが、当時の日本におけるデータ通信の環境はとても遅れていました。

DSLは序々に大容量（高速）化し、最近では数十メガbpsなどは当たり前です。それどころか1Gbps 強の製品も現実に存在します。

DSLのシステムは（DSLに限りませんが）、伝送距離は長いほど伝送容量（速度）は小さく（遅く）なります。

DSLは、従来のアナログ電話回線に使われるツイストペア・ケーブル (twisted pair cable) を使って信号を伝送します。伝送距離が伸びるにしたがって伝送容量（速度）は低下しますが、このことはシャノン容量を表す計算式が直接ではないものの、理由を明確に示しています。

参考記事

「シャノン容量」については「伝送路容量（通信路容量、速度）」をどうぞ。

伝送容量（速度）が低下する主な要因は、信号の減衰です。長距離では信号レベルが小さくなるからです。

では、なぜ信号レベルは小さくなるのでしょうか？

その理由は、伝送路の直流抵抗やその他の導体損失 (conductor losses)、誘電損失 (dielectric losses) などにより、信号の強度（電力、単位はワット）は送信端からの距離と共に序々に失われます。

伝送路の損失はワイアの太さにより変化します。ワイアは太いほど小さな損失で済みます。

参考

ワイアやケーブルの損失については「ケーブルやコードの損失」をどうぞ。

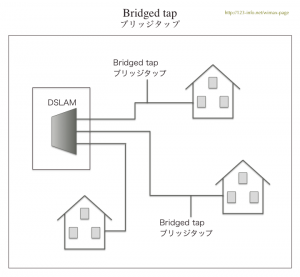
出発した信号が最終目的である自宅のADSLにたどりつくまでには、途中の様々な経路を通過します。ここで問題にしているのは、最寄りの電話局に設置してあるDSLAM（ディースラム、Digital Subscriber Line Access Multiplexer、下記「ブリッジタップ　bridged tap」の図で説明）からの経路です。

DSLに到達する信号の大きさは計算で求めることができます。計算式を最も単純化するために簡単にしたのが次の回路です。ケーブルの影響で信号が減衰することを直感的に知ることができます。

備考

回路図のシンボルは最も単純化した場合です。抵抗成分は、実際にはすべてリアタクンス(reactance)で表す必要があります。

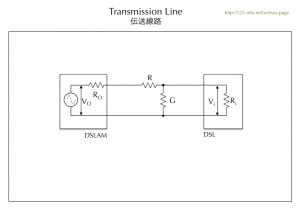
DSLにたどりつく信号の大きさViは
　　Vi=Vo \frac{(G // R_i)}{Ro + R + (G // R_i)}
ここで
　　G // R_i= \frac{1}{G} + \frac{1}{R_i}

線路抵抗Rは電話局からの長さで変化しますが、遠いほど増大します。損失Gの要素も変化しますが、大きく影響するのは線路抵抗Rです。ケーブルが長いほど信号が小さくなる理由はこれで分かります。

	シンボル	意味
	Vo	出力電圧　Output voltage
	Ro	出力抵抗　Output resistance
	R	線路抵抗　Line resistance
	G	損失　Loses
	Ri	入力抵抗　Input resistance
	Vi	入力電圧　Input voltage

現実の回路は、伝送線路−1のように単純ではありません。

信号はインダクタンスとキャパシタンスの影響も受けます。周波数により変化しますが、高い周波数ほど減衰する特性を示すことが分かります。

もう少し現実の回路に近づけると次のように表すことができます。

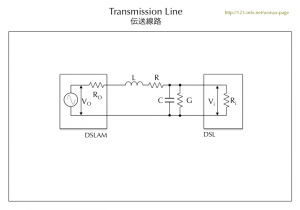
説明

LとCは伝送線路のインダクタンスと容量成分で、Gはラインの抵抗成分以外の損失を表します。損失には誘電損失 (Dilelectric loses) やその他の要素があります。（ラインの抵抗成分も損失の一種です。）

この回路では、DSLにたどりつく信号の大きさViは
　　Vi=Vo \frac{(C // G // R_i)} {Ro + \omega L + R + (C // G // R_i)}
ここで
　　C // G // R_i= \frac{1} { \frac{1}{\omega C}} + \frac{1}{G} + \frac{1}{R_i}, \hspace{7pt} \omega= 2 \pi f

現実の伝送線路を等価回路で表すと、はるかに複雑です。

伝送線路の部分は、図で示す成分がたくさんつながった状態で表現することができます。（図は、3組だけ書いてあります。）

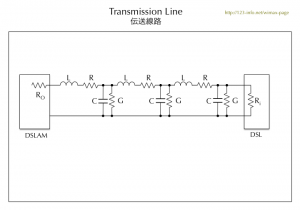
ADSLの伝送路容量（通信路容量、伝送速度）を下げる他の原因

アナログ電話回線において、伝送容量（速度）を下げる要因は、ケーブル単体の特性以外に、まだ他にもあります。

ブリッジ・タップ (bridged tap) は電話網の工事をするときに、加入者を見込んでケーブルを施設しておく「分岐」です。電話網では扱う周波数が低く、分岐はまったく問題にはなりません。DSLで扱う周波数帯域では、分岐のところでインピーダンスは大きく乱れ、伝送容量（速度）に悪い影響をもたらします。

ブリッジ・タップ　bridged tap

解説

DSLAM　Digital Subscriber Line Access Multiplexer

DSLAMは、モデムの集合体です。詳しい解説はありませんが、「モデムとは (ADSL)」を参考にどうぞ。

参考記事

DSLで扱う周波数ではなぜインピーダンスは乱れるのか、理由は距離と波長の関係にあります。次の記事を参考にどうぞ。（分岐の説明は、ありません。）
伝送路の仕組み［１］ー 距離と形状
伝送路の仕組み［３］ー 伝送路の特性

マイクロ波（300MHz〜3THz）のような高い周波数を扱う回路でも、分岐が必要なことは普通にあります。高い周波数を扱う回路では、分岐の部分でインピーダンス・マッチング (impedance matching) の処理を行うのは常識です。でないと所定の性能を維持できません。しかし、電話網では、扱う周波数が低いことからこんなことは気にも留めません。ところが、DSLは電話では気にしなかった高い周波数を扱うので、回線の途中に分岐があると問題が起こるのです。

伝送路容量（通信路容量、伝送速度）とツイストペア・ケーブルの距離

アナログ電話回線は、ツイストペア・ケーブル (twisted pair cable) を使用します。

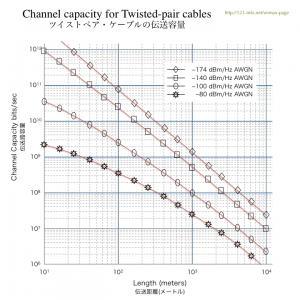
次の図は、ツイストペア・ケーブルの長さに対する伝送容量を計算し、グラフにしたものです。(※１)　この図では、送信電力を 16dBm (=40mW) にした条件で計算してあります。

dBmの計算

「0dBm　0デシベルミリワット　0ディービーエム」は電力（単位はワット）を表現する方法で、0dBm＝1mW は約束事です。

電力の16dBは、16dB＝10^(16/10)＝10^1.6＝39.81（倍）したがって、16dBm＝39.81mW＝約40mW です。

dBの計算は、対数と指数を扱うため誤差を伴うのが普通で、ほとんどの場合は概算で十分です。（もし、誤差を気にするようなら、その割合がどれほどなのか計算してみてください。普通は無視できるはずです。）

dBで表現する利点は、複雑なかけ算と割り算の代わりに足し算と引き算で計算できることです。いくつかの値を覚えておくと、暗算で簡単に計算できます。

16dB＝10dB +6dB　電力の場合は次の表から、10dB＝10、6dB＝4、したがって16dB＝10×4＝40（倍）

	電力 ワット	電圧（電流）
3dB	約2（1.9953）	約\sqrt{2}＝1.414（1.4125）
6dB	約4（3.9811）	約2（1.9953）
10dB	10	約3（3.1623）
20dB	100	10

4本中の最も上のプロットは、現実には実現できませんが、たとえば、距離 1キロメートル (10³m) で 1Gbps (10⁹bits/sec)を超える容量（速度）を得られることが分かります。（DSLでもです！）

伝送容量と距離

図の補足説明

4本のプロットは、ノイズレベルの条件を変えて、4種類の特性を表します。

最も上のプロット (-174dBm/Hz) は、最も低いノイズレベルの条件で、ケーブルにサーマルノイズ のみが存在するときです。現実にはこの状態を実現することは不可能です。（電波暗室のように、ほぼ完全にノイズを遮断できれば話は別です。）この条件では、1Km (10³m) の距離では1Gbps ((10⁹bits/sec) を少し超える容量（速度）に達することが分かります。

最も下のプロット (-80dBm/Hz) は、かなり現実の環境に近いと考えられるノイズレベルの条件です。この条件では、1Km の距離では20Mbps (2×10⁷bits/sec) を少し超える容量（速度）に達することが分かります。

AWGN　Additive White Gaussian Noise

「AWGN」は、ノイズが全くないところに、ホワイトガウスノイズを付加した条件を意味します。

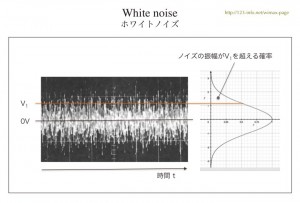
「ホワイトノイズ」は、あらゆる周波数成分で均一の強度から成るノイズのことです。あらゆる周波数成分を含むことから、色にたとえて「ホワイトノイズ」の表現を使います。

ガウスノイズ (Gaussian Noise) は、瞬時振幅を時間領域（タイムドメイン　time domain）で観測したとき、正規分布 (Normal distribution、ガウス分布　Gaussian distribution) を示すノイズです。

これは少し難しい表現かと思います。ノイズを観測するとき、ある瞬間の次の瞬時値を予測することはできませんが、振幅は大きくなったり小さくなったりし、さらに、プラスとマイナスの両方に変化します。長時間の平均では 0ボルト近辺の値が最も多く、グラフに描くと正規分布の特性を示します。

ホワイトノイズ　white noise

サーマルノイズ

抵抗が存在するところには、サーマルノイズ (thermal noise) が発生します。大きさは計算で求めることができます。現実のワイアはどんなものでも抵抗が存在しますから、サーマルノイズが発生します。

どんなに超低ノイズの回路でも、一定レベルのサーマルノイズは必ず存在します。絶対零度（0°K、-273℃）にでもしない限り、ノイズレベル0にすることはできません。もっとも、この温度で動作する回路は存在しないでしょう。

文献等では「サーマルノイズ」を「熱雑音」と表記するものがありますが、「雑音」を耳に聞こえる可聴帯域の「音」で定義するならば適切ではありません。「ノイズ」は可聴帯域を超えるはるかに広い帯域にわたり分布します。ここではあえて英語のカタカナ読みで表記します。

サーマルノイズの大きさ

サーマルノイズの実効値 (RMS) 電圧は次の式で計算できます。
N=\sqrt{4KTR\Delta{f}} (V)

ここで、
K=1.61\times{10^{-23}} (W・s/°K)　ボルツマン定数　Boltzmann constant
T (°K)　絶対温度、R (Ω)　抵抗値、\Delta{f} (Hz)　帯域幅

参考資料

※１
Fundamentals of DSL Technology
P. Golden, H. Dedieu, K. Jacobsen　共著　2006年　Auerbach Publication　刊